场上花 3h 硬造了一个奇怪的思路。会比官方题解绕一些。

题意：一个排列 $p$ 中有些数已经固定。给定 $k\in[0,n)$，求不存在 $i\neq j$ 满足 $p_i$<$j+k$ 且 $p_j$<$i+k$ 的排列个数。$n\le 8000$。

即，所有 <$p_i-k$ 且 $\neq i$ 的 $j$ 的 $p_j$ 都不能 $>i+k$。

一种直觉是把 $p_i$ 全部减去 $k$，就可以转化成 $k=0$ 但排列值域偏下的情况。

先做朴素的 $k=0$。即所有 <$p_i$ 的 $j\neq i$ 都不能 $p_j>i$。

看到 $i,p_i$ 同时出现在一条关系里，可以考虑画到图上刻画，即 $i\to p_i$ 连边形成若干个环。称从左往右连的边为正向边，右往左为反向边，自环两边的性质都有。原题的限制此时形如：

• 限制 A：一条正向边 $x\to y(x$<$y)$ 限制了 $[1,y)$（且不为 $x$）出发的边的终点都要在 <$x$ 的区域；
• 限制 B：一条反向边 $y\to x(x$<$y)$ 限制了 $[1,x)$ 出发的边的终点不能在 $>y$ 的区域。

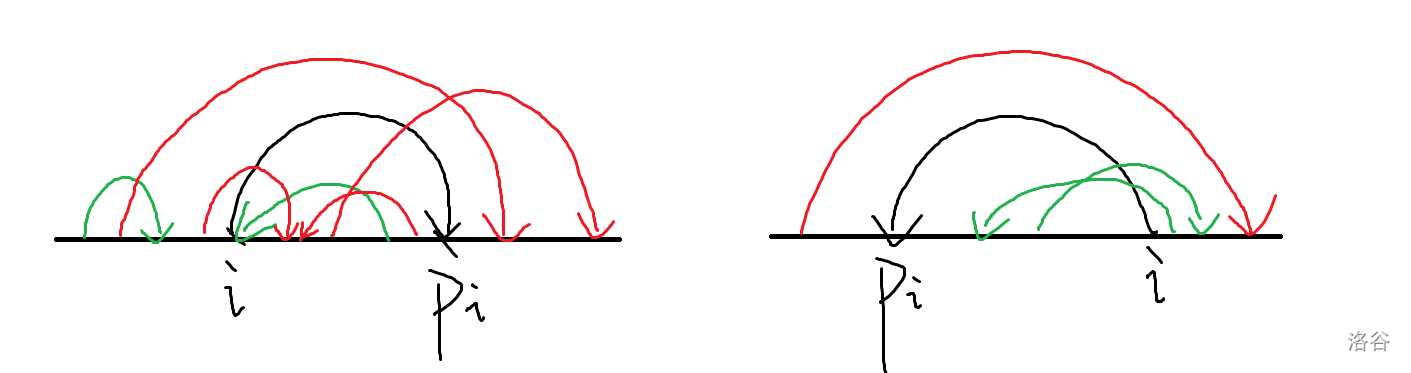
绿边是合法的，红边是不合法的。

由限制 A 得出，如果有一条正向边 $x\to y$，那么整张图上唯一能从 <$y$ 的点连到 $\ge y$ 的点的边，就是这条 $x\to y$。由此可得所有正向边覆盖的区域只会在端点处相交。那么一个环内的正向边一定是连续出现的，使得反向边也在环内连续出现。更进一步地，每个环覆盖的区域都不会相交。所以只要能确定每条正向边，整个图都是确定的了。反向边只能按顺序接回去，剩下啥都没有的位置填上自环。

此时由限制 B，不能有任何反向边被一条正向边完全覆盖（在端点相交不算）。也就是不能有一条正向边的长度大于 $2$。满足以上这些条件的排列就是合法的。

这就是一个 $k=0$ 的合法 $p$。

容易计算无初值的情况，有初值需要进行一些细节处理，略去。

然后考虑 $k>0$。

这里再对着排列环刻画的话就太困难了。于是这时可以使用上面提到的思路：把所有 $p_i$ 减 $k$，就转化为了 $k=0$ 的情况。那么放到图上就是把所有边的终点往左平移 $k$。

然而经过实践会发现往左平移 $k+1$ 然后做 $k=-1$ 的情况是更加合适的选择，原因稍后说明。

此时这个图就不是由环组成的了，更换一种刻画：考虑一个二分图，左部点为 $[1,n]$，右部点为 $[-k,n-k-1]$。这时的排列可以看成二分图上的一个完美匹配。正向边和反向边还是一样表示从左到右和从右到左，垂直的边算正向边（因为这里相当于是 $k=-1$，垂直边并不具有反向边的性质）。

$k=-1$ 意思就是，所有 $\le p_i$ 的 $j\neq i$ 都不能 $p_j\ge i$。和 $k=0$ 时类似地得到：

• 限制 A'：一条正向边 $x\to y(x$<$y)$ 限制了 $[1,y]$（且不为 $x$）出发的边的终点都要在 $\le x$ 的区域；
• 限制 B'：一条反向边 $y\to x(x$<$y)$ 限制了 $[1,x]$ 出发的边的终点不能在 $\ge y$ 的区域。

由此得：

• 限制 C：正向边覆盖的区域完全不交（并且不能有一对左右部点分别被两条正向边取到）；
• 限制 D：反向边覆盖的区域不能被正向边完全包含（取到同一对左右部点也算作包含）。

只要这个排列对应的图满足限制 C 和 D，它就可以满足原题限制。注意边界条件和 $k=0$ 不一样。

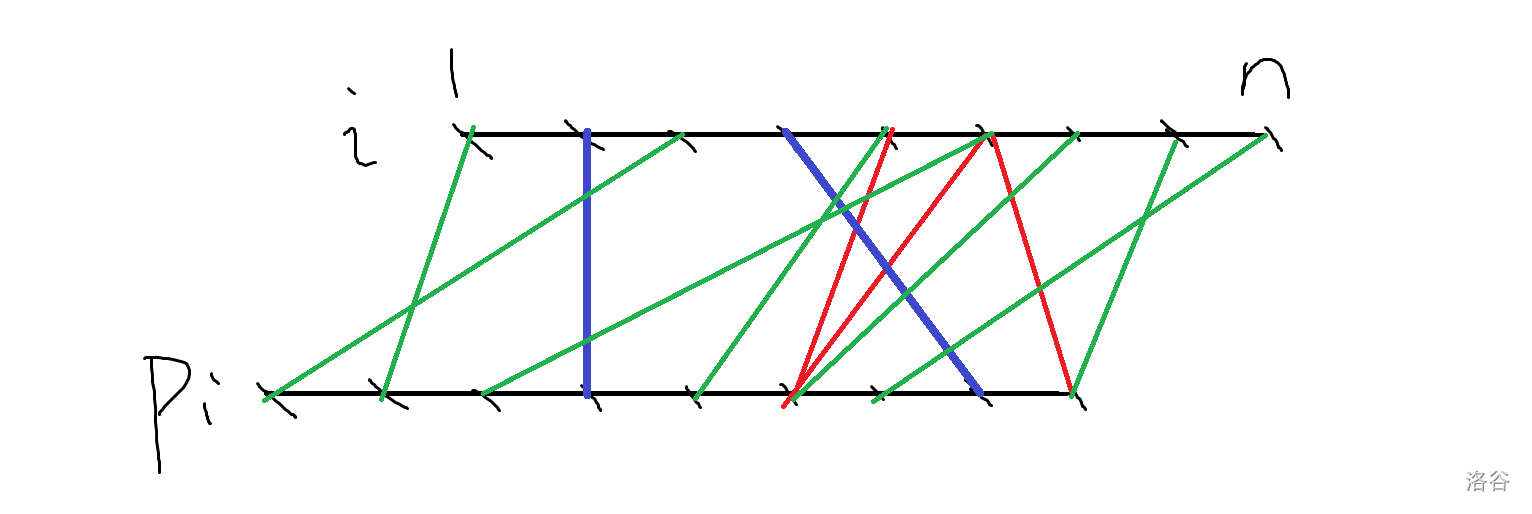
这是一个原本 $k=1$ 的二分图。蓝边是正向边，红边是确定了这些蓝边的情况下某些不能出现的边，绿边是一组合法的反向边匹配方案。

假设我们已经把所有正向边都定了下来，考虑反向边有多少种匹配方案。可以发现，每个未被正向边占用的左部点能匹配到的右部点一定是一段前缀（保证其是反向边，并且不会被一条前面过来的正向边盖住导致触发限制 D）并且，这个前缀的长度随起点位置递增。那设第 $i$ 个可用起点能匹配到的前缀长度为 $w_i$，方案数就是 $\prod(w_i-i+1)$。

考虑正向边没定的时候怎么办。DP。$dp_i$ 表示前面 $i$ 个起点已经匹配完毕，并且前面没有正向边伸到 $>i$ 区域的匹配方案数。（按理来说这里应该要设一个 $j$ 表示正向边条数，但实际推导过后可以发现并没有转移系数用到它。）如果 $i$ 是一条普通的反向边就直接 $dp_i\gets (k+1)dp_{i-1}$（$i$ 之前一定恰好有 $k+1$ 个终点还没被占用），否则我们枚举 $j$ 开一条从 $j\to i$ 的正向边，然后算上 $(j,i]$ 出发的所有反向边的方案数。容易知道是 $dp_i\gets (k+1)^{\underline{i-j}}dp_{j-1}(j\le i)$。即这一段所有的反向边都必须连到 <$i$ 的位置，不然就会触发限制 D。

• 这个地方如果是一开始想的往左平移 $k$ 的话就会发现问题：左右部点微妙地错开了。在 $k=0$ 的限制下，右部点 $j$ 可能已经被前面的一条正向边占用，而左部点 $i$ 却并没有受限制 D 的影响，它反倒还可能是下一条正向边的起点。所以平移 $k+1$ 是更加直观的方法。
• 本质上应该就是把 $>$ 改成 $\ge$ 会变得方便许多。

于是可以 $O(nk)$ 获得没有初值的分数。

有初值的话需要添加一些细节。如果一条正向边被固定，那就相当于这一段区间必须只能做第二种转移。如果一条反向边被固定，它会导致上面的很多系数变化，减去一个类似“这段区间里有多少个终点被后面来的一条固定反向边用掉了”的东西，同时可能导致一些正向边变得不合法。总之也是 $O(nk)$ 的。

笔者水平有限，逻辑可能有繁杂或详略不得当之处，欢迎交流。